1. Introduction

Big data have revealed many positive and statistically significant correlations, some of which were quite unexpected, and this will no doubt continue into the foreseeable future [1-6]. Since given a large enough sample, highly improbable things will occur (people do win lotteries), these correlations could be coincidences or they could have other diverse and relevant meanings. The author [7] recently outlined several methods for adapting to this new environment. The present paper implements some of those methods by introducing algorithms for dealing with the intractable propositions and fuzzy correlations arising from big data.

2. Automated theorem proving

One method of dealing with big data requires searching through a database of axiom sets. As noted in the sequel, this task can literally take centuries when it is done manually based only upon intuition. However, a computer could do such a search very quickly.

2.1. Algorithm

Consider the equation:

rn + sn = tn (1)

where r, s and t are positive real numbers and n is a positive integer. Recall that Ramsey's theorem for pairs [8] states that almost all theorems are equivalent to a major axiom set. Let A(ℜ) be the axiom set for the real numbers. From A(ℜ) we can state all of the following about Equation (1):

Lemma 1. Equation (1) has infinitely many solutions since if r and s are any positive real numbers and n is a positive integer, then (rn + sn)1/n is a positive real number t.

Lemma 2. If, and only if, n is even, then Equation (1) has solutions in which the positive bases r, s, and t, can be replaced by their negative counterparts: -r, -s and -t.

Lemma 3. If n=2, then n is even.

Lemma 4. The converse of lemma 3 is false.
Recall also that Gödel's incompleteness theorem [9] states that not all propositions can be decided using just A(ℜ). As an example, let us modify the hypotheses for Equation (1) by restricting r, s and t to be positive integers. Since Fermat's last theorem (FLT) has been proved [10], lemmas 1 and 2 no longer hold. Hence, to prove FLT, a supplemental axiom set is required. From [10] it is clear that the additional axioms needed concern modular elliptic curves. As is well-known, the axioms needed for many problems in modern science cover multidimensional spaces with negative, flat, and positive curvature, including especially imaginary and complex numbers.

FLT is an instructive example since its history can be predictive. Despite diligent efforts on the part of professional and amateur mathematicians alike, it took over three centuries after Fermat [11] first introduced his so-called last theorem before a viable method of proof was published by Wiles [12]. Even then, there was a gap in the proof that was circumvented with the help of Taylor, as described in [10]. The proof is voluminous and involves complex and arcane arguments concerning modular elliptic curves. Clearly, the problem was that those who struggled for centuries to prove FLT did not know which axiom sets to use. We can expect the same problem to exist in the age of big data unless this problem is properly automated since big data will be used to infer (as opposed to imply) propositions that require multiple axiom sets and, thus, cannot be proved using the standard methods for automated theorem proving [13-18]. The algorithm for achieving this is depicted in Fig. 1.

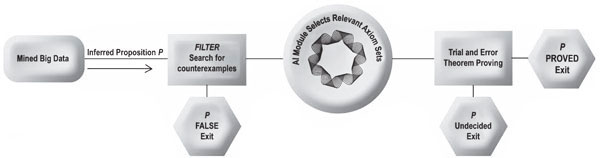
Fig. 1. Algorithm for automated proving of intractable and fuzzy theorems.

2.2. The importance of context awareness

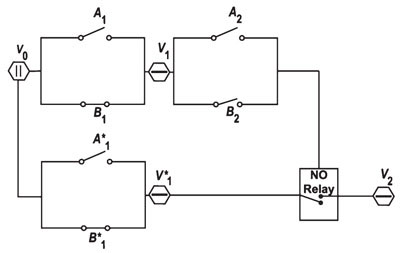
In selecting the appropriate axiom sets, the AI module must rely on context awareness, which cannot be merely intuitive but must be rigorous. This is easily demonstrated to electrical and electronics engineers as shown by the circuit in Fig. 2. Although physically it is a simple analog circuit, it becomes a model for Equation (1) when the following modeling
parameters are used:

1. V* 1 on means that Equation (1) has a solution with positive bases. (This assures consistency with lemma 1 because the context has B*1 on.)

2. Iff A1 is turned on, then q=2.

3. Iff A2 and V1 are both on, then q is even. (This means that ifA2 is on, then q is even because the context has B1 and, therefore, V1 on. However, the fact that q is even does not imply q = 2, which requires that A1 be turned on.)

4. V2 on means that Equation (1) has a solution in which the positive bases r, s and t are replaced by their negative counterparts -r, -s and -t. (Consistent with lemma 2, when B2 is off, V2 is on iff A2 is also on.)

However, if we change context such that B1 is off, then we have the context for FLT. But since Lemmas 3 and 4 still hold, this is a contradiction, demonstrating that a supplemental axiom set is needed for the new context.

Fig. 2. V0 is a power source. The Vi are power buses with V2 the consequential effect. The Ai and Bi are binary switches. The Bi are the context and the Ai are causal antecedents.With B2 off, the NO (normally open) relay completes a circuit between V0 and V2 only if A2 is on.

2.3. Undecidable theorems

When the algorithm depicted in Fig. 1 stops because no counterexample has been found nor could the trial-and-error theorem proving module find a proof, then we have a fuzzy proposition P that appears empirically to be true but we cannot know for certain. This may be because the AI module has an inadequate database of axiom sets or because proposition P is inherently undecidable.

Let p(F) be the probability that P is false, and let p(T) be the probability that P is true. Although false P and true P are mutually exclusive, we do not have the Boolean case in which p(F) + p(T) = 1 because there exists a third truth value: undecidable P. Consequently, it is convenient to use the probability u(AI) that P is true but the AI module has an inadequate database of axiom sets,

u(AI) = [0, 1] (2)

The correct value for u(AI), zero or one, can be estimated using the value of a continuous variable 0 ≤ u * (AI) ≤ 1, for example 0 << u * (AI) or u * (AI) << 1.

Metric for AI module: An estimate u * (AI) of u(AI) should be calculated for the AI module in Fig. 1.

3. Extracting knowledge from stochastic data

Often big data reveal a positive and statistically significant correlation between a system condition c and a system state δ that reflects a risk factor. This has nothing to do with causality since a risk factor is not a necessary condition for δ, much less a sufficient condition. Indeed, this is virtually tautological.

Axiom 1: If a system is in state δ without having condition c, then c is not a necessary condition for δ.

Axiom 2: If a system has condition c and is not in state δ, then c is not a sufficient condition for δ.

3.1. The public health example

The disease malaria gets its name from two medieval Italian words meaning "mal" (bad) and "aria" (air). This is because inhaling swamp gas is a risk factor for malaria. It means a person is in close proximity to a swamp. Being in close proximity to a swamp increases the risk of being bitten by a mosquito. Being bitten by a mosquito increases the risk of being infected with Plasmodium falciparum. Being infected with P. falciparum is a necessary condition for malaria [19]. The other necessary condition is being susceptible to developing the disease when so infected and not protected by the HbAS allele [20]. The conjunction of all necessary conditions is the sufficient condition or cause of malaria.

For centuries, the risk factor of inhaling swamp gas was deemed to be the cause of malaria. The cause of malaria could not have been known until the advent of the microscope, the germ theory of disease and the science of microbiology. However, because of Axioms 1 and 2, it could have been known from the very beginning that inhaling swamp gas was not the cause of malaria. There were people with malaria who had never inhaled swap gas, and there were people who had lived and died without ever having malaria despite the fact that they had inhaled swamp gas. In other words, the confusion over malaria was not due to a lack of information but was due to a lack of rational thinking.

Needless to say, it is good public policy for public health officials to educate the public about risk factors in order to promote healthy lifestyles, such as not smoking. But confusing the risk factors for a disease with the necessary conditions for that disease causes harm in two ways. First, necessary conditions must be recognized and addressed in order to develop effective treatments for a disease. Secondly, it causes false hope, as when people believed they could not get malaria if they never inhaled swamp gas.

Again, smoking is a good example. As is well known, governments and public health officials in the western democracies have been making a persistent effort to convince the public that smoking "causes" lung cancer.Yet, there are many people who have died of lung cancer despite the fact that they were never exposed to tobacco smoke; furthermore, there have been many smokers who lived their whole lives and never had lung cancer [21, 22]. This impairs cancer research, which depends upon knowing the necessary conditions for cancer. Indeed, it puts medical researchers in the difficult position of having to report conclusions that are contradicted by the data their studies generate [23]. It also leads people to believe incorrectly that if they never smoke, then they cannot get lung cancer. One example is the late nonsmoker Dana Reeve, widow of the late actor Christopher Reeve, whose terminal lung cancer surprised her and her family [24].

3.2. Algorithm

Axioms 1 and 2 can be cast in set-theoretic terms. In a given universe U of systems, let c be a system condition and let δ be a system state such that an analysis of mined big data reveals a positive and statistically significant correlation between c and δ. Let C be the nonempty set of all systems in U having condition c and let S be the nonempty set of all systems in U occupying state δ. Let φ denote the empty set.

Theorem 1. If S - {C ∩ S} /= φ, then c is not a necessary condition for δ.

Theorem 2. If C - {C ∩ S} /= φ, then c is not a sufficient condition for δ.

Theorem 3. If c is neither necessary nor sufficient for δ, then c is a risk factor for δ.

For most practical purposes, we only need to be concerned with differentiating risk factors from necessary conditions. Sufficient conditions are the conjunction of all necessary conditions. Some of these necessary conditions will be implied by context, such as having a system in U. For example, a necessary condition for a primate infected with HIV to have AIDS is that the primate be human [25]. We take this for granted when investigating HIV/AIDS. The necessary conditions that matter are the ones we can do something about. A useful decision tree or algorithm in this regard is depicted in Fig. 3.

For the benefit of one of four reviewers, the author is compelled to point out that the word "algorithm" is not restricted to coding but can refer more generally to schema or methodologies. The Oxford dictionary defines an algorithm as "a process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer." At the beginning of this subsection, it was noted that Axioms 1 and 2 can be cast in set theoretic terms. A careful inspection of Fig. 3 will reveal that this is precisely what the algorithm or set of rules shown in Fig. 3 is doing. This is related to the example from healthcare by the fact that the example does not adhere to Axioms 1 and 2. As explained formally by Theorems 1 through 3, inclusively, if a person has a disease but does not have a condition, then that condition is not a necessary condition for the disease. This is what the English word "necessary" means. Likewise, if a person has a condition but not a disease, then the condition is not a sufficient condition for the disease. This is what the English word "sufficient" means.

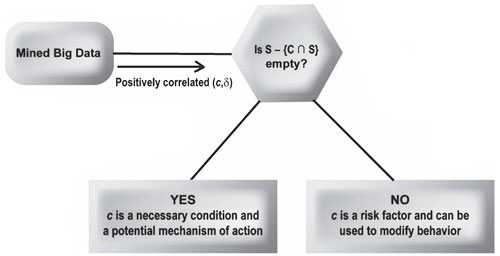
Fig. 3. Decision tree for positive and statistically significant correlations revealed by big data.

4. Conclusions

Crawford [26] and Boyd [5], among others, ask if big data is a disruptive force that will fundamentally change what theword "research" means. Indeed, as shown here, big data may eviscerate science by interpreting positive and statistically significant correlations as reflecting causal factors when they are, in truth, risk factors or even the rare coincidence. As also discussed here, this problem has impaired the public health sector for centuries, even before the advent of big data. But this problem is easily resolved with the decision tree depicted in Fig. 3, which imposes rigorous, logical thinking.

Ramsey's theorem for pairs [8] admits to a few theorems that require more than one axiom set for proof. When "relatively few" are multiplied by the large size of big data, the absolute number becomes significant. Hence, the need to update automatic theorem proving with the unique algorithm depicted in Fig. 1. To conclude this paper with the same observation as the author's [7], the need for that algorithm confirms Gödel's theorem that A(ℜ) is not always a sufficient axiom set. It also circumvents the problem by employing the unique AI module. Beyond preserving traditional science in the age of big data, this could open new horizons for researchers.

In conclusion, the contribution of the present paper is to review some of the serious societal problems caused when Axioms 1 and 2 are not recognized, and then to introduce an original, algorithmic solution to such problems.

References

[1] R. Kitchin, Big Data, New epistemologies and paradigm shifts, Big Data and Society (2014), http://journals.sagepub.com/doi/abs/10.1177/2053951714528481

[2] K. Mayer-Schonberger, Cukier Big data: A revolution that will transform how we live, work, and think, Houghton Mifflin Harcourt, Boston and New York, 2013.

[3] M. Swan, The quantified self: Fundamental disruption in big data science and biological discovery, Big Data 1 (2013), 85-99.

[4] F. Provost and T. Fawcett, Data science and its relationship to big data and data-driven decision making, Big Data 1 (2013), 51-59.

[5] D. Boyd and K. Crawford, Critical questions for big data: Provocations for a cultural, technological, and scholarly phenomenon, in: Information, Communication & Society, Special Issue: A decade in Internet time: The dynamics of the Internet and society, 15, 2012.

[6] R.Y. Wang and D.M. Strong, Beyond accuracy: What data quality means to data consumers, Journal of Management Information Systems 12 (1996), 5-33.

[7] A.D. Allen, When axioms collide: An unfulfilled opportunity to advance knowledge for man and machine through automated reasoning, International Conference on Computer Systems and Communication Technology, Shenzhen, China, 2016.

[8] P.A. Cholak, C.G. Jockusch and T.A. Slaman, On the strength of Ramsey's theorem for pairs, Journal of Symbolic Logic 66 (2001), 1-55.

[9] R.M. Smullyan, Gödel's Incompleteness Theorems, Oxford University Press, Oxford, UK, 1992.

[10] G. Faltings, The proof of fermat's last theorem by R. Taylor and A. Wiles, Notices Amer Math Soc 42 (1995), 743-746.

[11] T. Heath, Diophantus of Alexandria, Second Edition, Cambridge University Press, Cambridge, UK, 1910. Reprint by Dover Books, New York, NY, 1964.

[12] A.Wiles, Modular elliptic curves and Fermat's last theorem, Ann of Math 141 (1995), 443-551.

[13] J. Furnkranz and M. Kubat, Machines that learn to play games, in: Advances in Computation: Theory and Practice 8, Nova Science, New York, 2001.

[14] H.B. Hwarng and N.F. Hubele, Boltzmann machines that learn to recognize patterns on control charts, Statistics and Computing 2(4) (1992), 191-202.

[15] A. Esuli and F. Sebastiani, Machines that learn how to code open-ended survey data, Inter J Market Res 52 (2010), 775-800.

[16] W.W. Bledsoe and D.W. Loveland (eds.) Automated Theorem Proving After 25 Years, American Mathematical Society, Providence, RI, 1984.

[17] J.R. Slagel, Automated theorem-proving for theories with simplifiers commutativity, and associativity, JACM 21 (1974), 622-642.

[18] A.J. Nevins, A human oriented logic for automatic theorem proving, JACM 21 (1974), 606-621.

[19] R.M. Packard, The Making of a Tropical Disease: A Short History of Malaria, John Hopkins University Press, Baltimore, MD, 2007.

[20] T.N.Williams, T.W. Mwangi, S.Wambua, N.D. Alexander, M.Kortok,R.W. Snowand K. Marsh, Sickle cell trait and the risk of Plasmodium falciparum malaria and other childhood diseases, J Infect Dis 192 (2005), 178-186.

[21] B. Meier, Judge voids study linking cancer to secondhand smoke, New York Times, 1998.

[22] J. Peres, No clear link between passive smoking and lung cancer, J Natl Cancer Inst 105 (2013), 1844-1846.

[23] R.A. Levy and R.B. Marimont, Lies, damned Lies & 400,000 smoking related deaths: Cooking the data in the fascists' antismoking crusade, Internet: https://www.sott.net/article/229156-Lies-Damned-Lies-400000-Smoking-related-Deaths-Cooking-the-Data-in the-Fascists-Anti-Smoking-Crusade (1998).

[24] Dana Reeve dies of lung cancer at 44. Internet: http://www.cnn.com/2006/SHOWBIZ/03/07/reeve.obit [March 8, 2006].

[25] J.M. Zarling, J.A. Ledbetter, J. Sias, P. Fultz, J. Eichberg, G. Gjerset and P.A. Moran, HIV-infected humans, but not chimpanzees, have circulating cytotoxic T lymphocytes that lyse uninfected CD4+ cells, J Immunol 144 (1990), 2992-2998.

[26] D. Bollier, The Promise and Peril of Big Data, Aspen Institute, Washington, D.C., 2010.

For the benefit of one of four reviewers, the author is constrained to point out the following: When a graphic illustration appears in a journal without a copyright notice and without a "Used with permission" statement indicating that a license has been granted by the copyright owner, then the graphic was created by the author expressly for the paper and the copyright has been transferred to the journal's publisher along with the text. This is the case for all of the figures in this paper.